Introduction to the BODMAS Rule
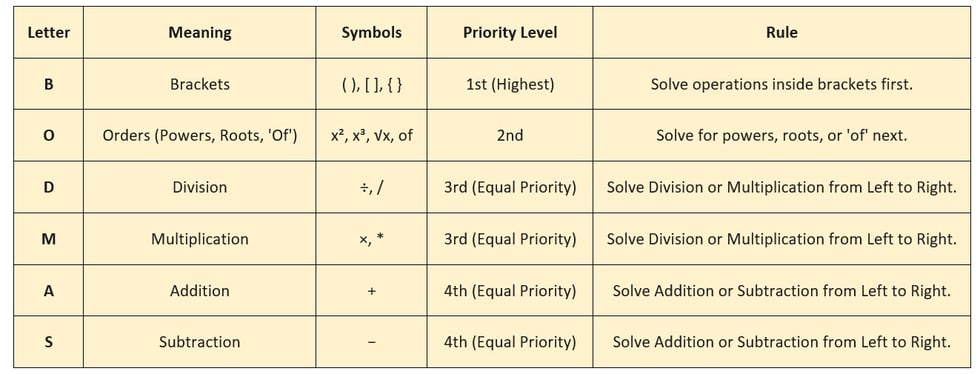
The BODMAS rule helps us solve math problems in the right order. It stands for Brackets, Orders (like powers or square roots), Division, Multiplication, Addition, and Subtraction—and we follow this order to get the correct answer.
Using BODMAS avoids confusion and mistakes, especially when expressions include different operations. It’s not just for school—BODMAS is useful in everyday tasks like budgeting or in fields like engineering and science.
Learning this rule early builds strong problem-solving skills and makes complex maths easier to handle later on. Let’s explore how BODMAS works and why it’s so important.
Example on solving BODMAS
Importance of BODMAS in Mathematics
BODMAS—Brackets, Orders, Division/Multiplication, Addition/Subtraction—sets the correct order for solving maths problems. It removes confusion and ensures consistent, accurate answers.
Without BODMAS, expressions like 6 + 2 × 3 could give different results. But using the rule, we solve multiplication first: 2 × 3 = 6, then add 6 + 6 = 12—avoiding errors.
This rule isn’t just for students. Professionals in fields like finance, engineering, and coding rely on BODMAS for clear, accurate calculations. It helps prevent mistakes and makes problem-solving more efficient.
Common Errors Without BODMAS
Skipping the BODMAS rule can lead to wrong answers. A common mistake is solving from left to right without thinking about the correct order.
Take 8 + 4 × 2. If you add first, you get 12 × 2 = 24. But BODMAS says multiply first: 4 × 2 = 8, then 8 + 8 = 16—which is the correct answer.
Another example is (5 + 3) × 2. Brackets come first, so solve 5 + 3 = 8, then 8 × 2 = 16. Ignoring the brackets could lead to completely different answers, especially in harder problems.
Following BODMAS helps students avoid these common errors and makes their calculations reliable.
Teaching BODMAS in Australian Schools
Australian schools teach BODMAS as part of the national curriculum. It helps students think clearly and solve problems in the right order.
Teachers use puzzles, real-life examples, and visual aids like flowcharts to explain how BODMAS works. Many also use digital tools and interactive apps that let students practise and get instant feedback.
By learning BODMAS early, students build confidence and develop strong maths skills that help in more advanced topics later on.
Practical Applications of BODMAS in Real Life
BODMAS isn’t just for the classroom. People use it in finance, construction, and computer programming every day.
In finance, BODMAS helps calculate things like compound interest accurately.
In architecture, it ensures building measurements and loads are calculated correctly.
In coding, programmers rely on BODMAS to make sure calculations in algorithms work as expected.
Getting the order wrong can lead to serious mistakes—so knowing BODMAS really matters in real life too.
BODMAS vs Other Rules (PEMDAS/BIDMAS)
You might hear other names like PEMDAS (used in the US) or BIDMAS (used in the UK). They all mean the same thing—just different words.
BODMAS = Brackets, Orders, Division/Multiplication, Addition/Subtraction
PEMDAS = Parentheses, Exponents, Multiplication/Division, Addition/Subtraction
BIDMAS = Brackets, Indices, Division/Multiplication, Addition/Subtraction
No matter which version you learn, they all help you solve problems in the same order. In Australia, we use BODMAS.
Conclusion
Learning BODMAS helps students solve maths problems the right way. It gives them a clear path to follow, avoids confusion, and builds strong problem-solving skills.
By practising BODMAS regularly, students gain confidence—not just in maths, but in everyday tasks that involve numbers. Whether you’re doing homework, saving money, or writing code, this rule makes sure your answers are right.
Stick with it, practise often, and you’ll be surprised how much easier maths becomes.
