Fractions, referred to as “a part of”, are a fundamental part of mathematics. They allow us to represent numbers that are not whole, facilitating a deeper understanding of quantities and relationships. In Sydney, students are engaging in the fascinating world of fractions, a fundamental concept in arithmetic. A fraction represents a part of a whole and can be expressed in two primary forms: in-line notation as a/b. In these expressions, ‘a’ is referred to as the numerator, while ‘b’ is the denominator.
Whether it’s through simple tasks, like sharing a pizza or measuring ingredients in cooking, fractions help us to grasp the concept of division and proportionality. In more advanced applications, fractions are essential in algebra, geometry, and even calculus, where they are used to solve complex equations and analyze functions. Mastering fractions is crucial for anyone looking to develop strong mathematical skills, as they serve as the building blocks for more advanced topics. Understanding fractions not only enhances our problem-solving abilities but also equips us with the tools needed to navigate everyday situations that involve division and sharing.
1. Simplifying Fractions
The GCD [Greatest Common Divisor] is the largest number that can evenly divide the numerator and denominator. When we divide the numerator and the denominator by the GCD, the fraction is reduced to its simplest form, making it easier to understand and work with.
In the following example, the GCD for the fraction 8/12 is 4. By dividing the numerator and the denominator by the GCD, we get the result 2/3.
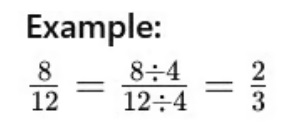
2. Adding Fractions
To add fractions effectively, it’s essential that the denominators are identical. When the fractions have the same denominator, you simply add the numerators together while keeping the denominator unchanged.
In the following example, if you have the fractions 1/4 and 2/4, you can add them by combining the numerators: 1 + 2 equals 3. Therefore, the sum is 3/4. If the fractions do not initially share a common denominator, you must first convert them to equivalent fractions that do. The example is shown below:

This process ensures accurate results when performing addition with fractions, making it a vital skill in mathematics. Understanding this concept lays a strong foundation for more complex operations involving fractions in the future.
3. Subtracting Fractions
Subtracting fractions is a straightforward process that mirrors the method used for adding them. To successfully subtract fractions, the first step is to ensure that both fractions have a common denominator. Once this is established, you can proceed by subtracting the numerators of the fractions while keeping the denominator unchanged. For instance, if you have the fractions 3/8 and 1/8, you would subtract 1 from 3, resulting in 2. The denominator remains 8, giving you a final answer of 2/8, which can be simplified to 1/4. Another example is shown below:

Remember that maintaining a common denominator is crucial for accurate subtraction, just as it is for addition, ensuring that the fractions are compatible for the operation.
3. Multiplying and Dividing Fractions
To multiply fractions, the numbers in the numerators are multiplied together to get the new numerator. Similarly, the denominators are multiplied together to find the new denominator.
For example, multiplying 1/2 by 3/4 results in (1 x 3) / (2 x 4), which simplifies to 3/8.
Dividing fractions, on the other hand, requires a slight adjustment. Instead of directly dividing, you multiply by the reciprocal of the fraction you are dividing by. For instance, to divide 1/2 by 3/4, you convert the division into multiplication by flipping the second fraction, resulting in 1/2 x 4/3. This gives you (1 x 4) / (2 x 3), simplifying to 4/6, which can be further reduced to 2/3. Understanding these processes is essential for effectively working with fractions in various mathematical contexts.