Parabola Theory, Formulae and Practice
Learn mathematics in a clear easy way with Aussie Math Tutor, your go-to destination for expert private math tutoring online. Our experienced tutors provide personalized instruction, helping you master complex concepts such as the Parabola—a U-shaped, mirror-symmetrical curve representing a quadratic relation on a graph.
Explore the Parabola theory, from understanding the standard equations, identifying maximum and minimum points, to learning about dilation effects.
PARABOLA
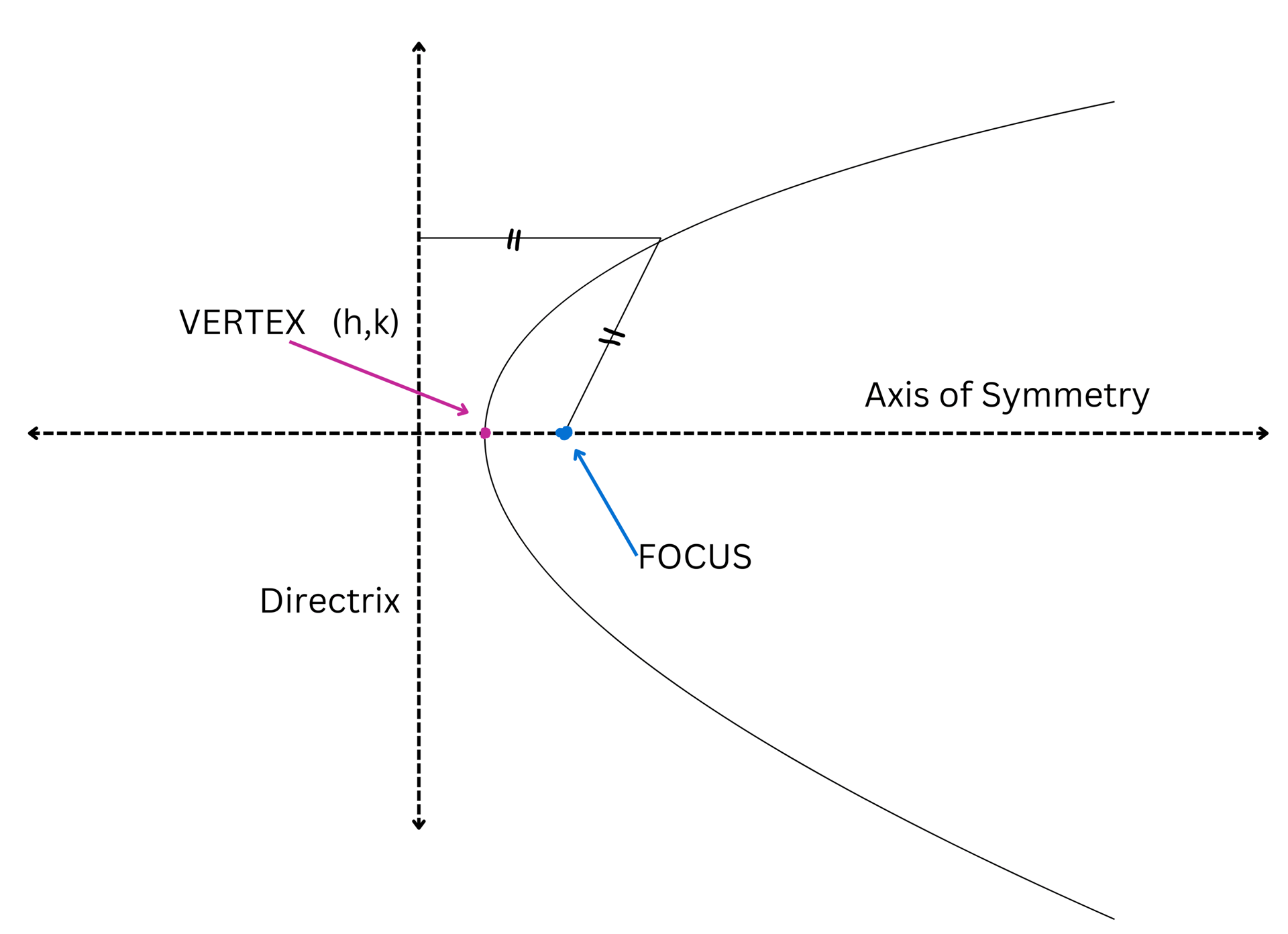
The Parabola represents a quadratic relation on a graph. It is a U-Shaped mirror symmetrical curve in which each point is equidistant from a fixed point (Focus) and a Fixed Line (Directrix) as shown in the below image:
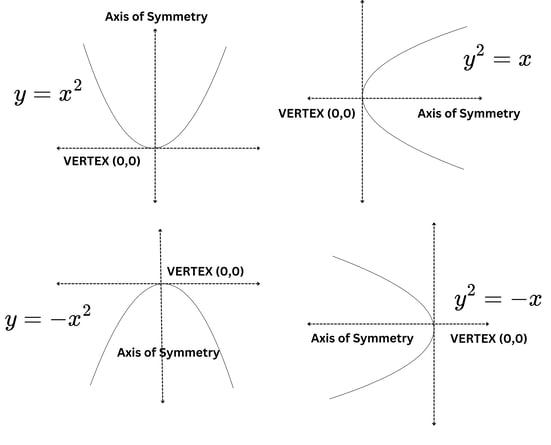
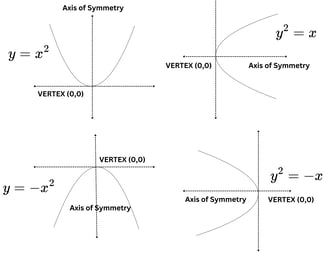
Standard Equations of a Parabola
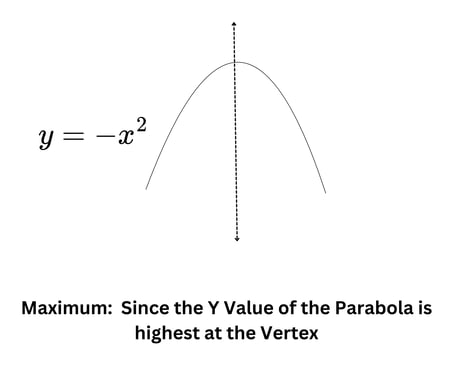
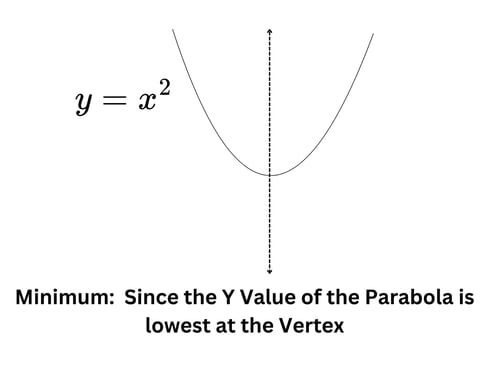
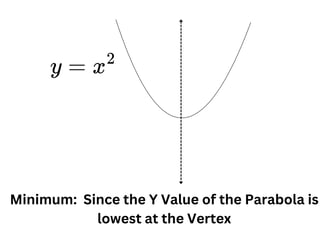
Maximum and Minimum in a Parabola
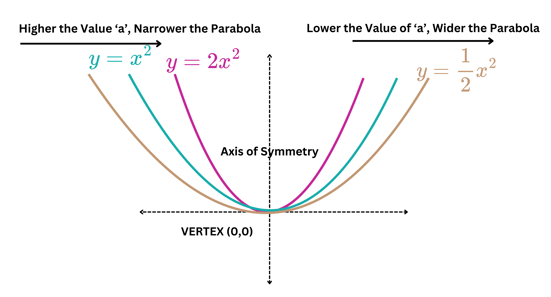
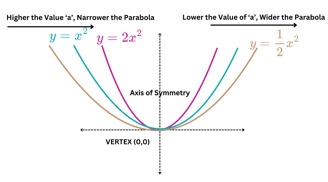
Dilation in Parabola
WhatsApp us at +61-0422 768 717
Love what you're learning? Level up with Aussie Math Tutor NSW. Join now!
1. Minimum or Maximum
2. Narrower or Wider than y=x
3. Whether it is Reflected in the X-Axis
4. Turning Point
5. Y-value when x=1
2
Find the Following for the below equations:
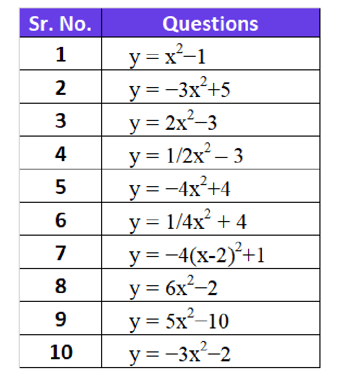
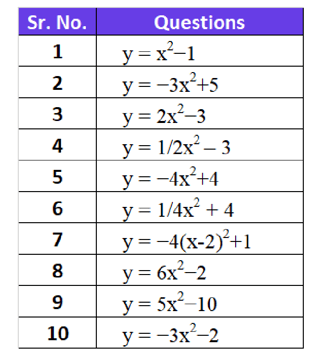
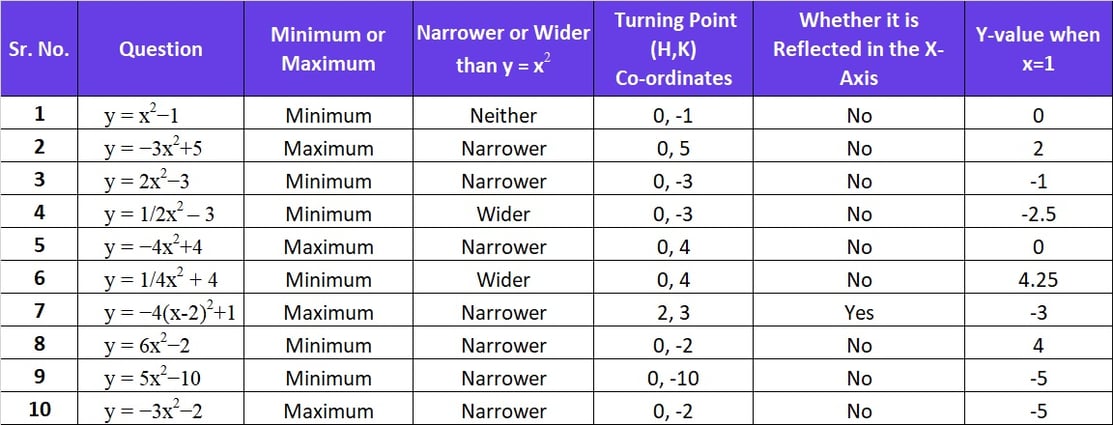
ANSWERS
How to Sketch a Parabola?
In order to sketch a Parabola, follow these steps:
Step 1: Determine the kind of U-shaped curve is the Parabola. Refer to the Standard Equations of the Parabola.
If a>0, the parabola opens upwards (U-shaped).
If a<0, the parabola downwards (inverted U-shaped).
Step 2: Find the y-intercept/s for the equation by substituting x=0 in the given equation. If there are two different solutions of y, it means that the equation intercepts the Y-axis at two different points. There may not be any solution as the Parabola may not intercept the Y-axis.
Step 3: Find the x-intercept/s for the equation by substituting y=0 in the given equation. If there are two different solutions of y, it means that the equation intercepts the Y-axis at two different points. There may not be any solution as the Parabola may not intercept the X-axis.
Step 4: If there are two solutions of y, find the mid-point to determine the Axis of Symmetry. Else find the mid-point from the two solutions of x. This is one of the vertex point as the vertex lies on the axis of symmetry.
Step 5: Using the midpoint in Step No. 4, substitute that value in the main equation to find the other co-ordinate of the Vertex.
Example on How to Sketch a Parabola
In order to sketch a Parabola, follow these steps:
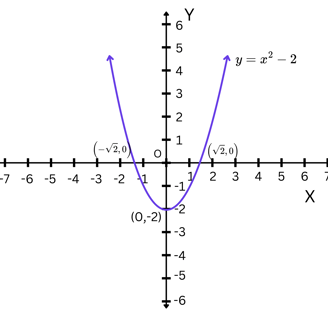
Step 1: Determine the kind of U-shaped curve is the Parabola. Here, a=1 > 0. Hence, the parabola opens upwards (U-shaped).
Step 2: Find the y-intercept/s for the equation by substituting x=0 in the given equation.
Hence, y=x - 2; y= (0) - 2 = -2.
So, the y-intercept is at the point (0, -2). Since there’s only one solution for y, the parabola intersects the y-axis at one point.
Step 3: Find the x-intercept/s for the equation by substituting y=0 in the given equation.
Hence, y=x - 2 ; 0=x - 2; x = 2; There fore x= +-sqrt(2)
Therefore, There are parabola intercepts the parabola at two points: (+sqrt(2), 0) and ( -sqrt(2),0).
Step 4: Since there are two solutions of y, we find the mid-point to determine the Axis of Symmetry.
Hence, [sqrt(2) - sqrt(-2)]/2 = 0/2 = 0. Therefore, x=0, which is the equation for the Y-axis, is the Axis of Symmetry.
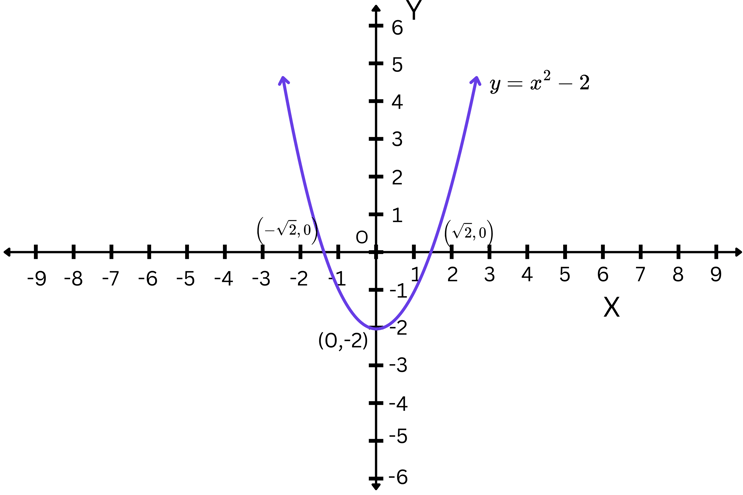
Step 5: Substitute x=2 in the main equation, we get y=-2. Hence, the Vertex is at (0,-2). Using the point, we will therefore plot the Parabola which is as follows:
Draw the Parabola for the equation y=x - 2
2
2
2
2
2
How to Write an Equation of a Parabola from a given figure?
To write the equation of a parabola from a given graph, you'll need to identify certain key characteristics of the parabola, such as its vertex, direction of opening, and possibly other points on the parabola. Here’s a general approach:
Steps to Write the Equation of a Parabola
Step 1. Identify the Vertex
The vertex (h,k) is the highest or lowest point on the parabola. If the vertex is visible on the graph, note its coordinates.
Step 2. Determine the Direction of Opening
If the parabola opens upwards or downwards, it will have the form of : y = a (x−h) + k.
If the parabola opens left or right (less common), it will have the form of : x = a (y−k) + h.
Step 3. Use Another Point on the Parabola
To find the value of a, substitute the coordinates of another point (x1,y1) that lies on the parabola into the equation. This helps in determining the stretch or compression of the parabola.
Step 4. Plug in the Values
Use the vertex and the point on the parabola to write the equation in its standard form.
2
2
WhatsApp us at +61-0422 768 717
Love what you're learning? Level up with Aussie Math Tutor NSW. Join now!
Email us at : info@aussiemathtutor.com.au
Contact Us
WhatsApp us at +61-0422 768 717
