Best Online Private Math Tutor

Proving Pythagoras' Theorem Using the Area Comparison Method

Explore the Pythagoras Theorem and its unique properties in 45-45-90 and 30-60-90 triangles in this blog Perfect for students and math enthusiasts, this tutorial breaks down the fundamentals and special characteristics of these right triangles, making complex concepts easy to understand.

MATH TOPICS

5/27/20241 min read

Pythagoras' Theorem is one of the most fundamental principles in mathematics, named after the ancient Greek mathematician Pythagoras. According to the theorem,

The Square of the hypotenuse IS EQUAL TO The Sum of the squares on the other two sides.

Mathematically, it is often expressed as:

Step-by-Step Proof of Pythagoras' Theorem Using the Area Comparison Method

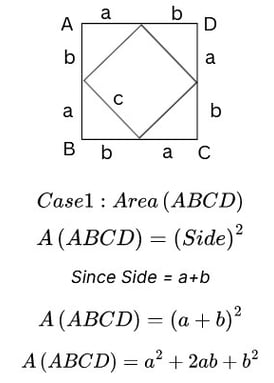
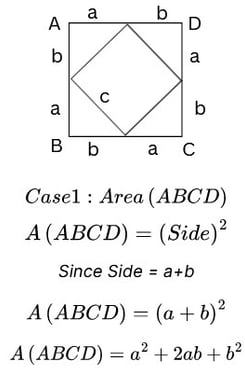
To prove the Pythagoras Theorem, we have drawn a square with side "c", inscribed in another square ABCD as shown below. Then we try to find the area of the square ABCD as shown blow

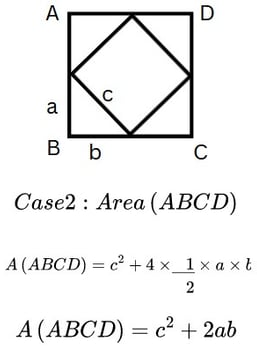
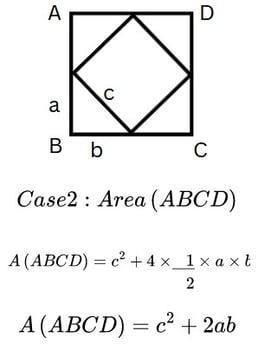
In Case 2, we add the area of the inner square and the area of the four congruent triangles as shown below:

Since both the areas of Case 1 and Case 2 are equal, we get the following equations, thus proving the theorem: